Capítulo 3 Quantmod

IMPORTATE: Aún no está del todo listo el formato en pdf, por lo que recomiendo verlo online.

El paquete quantmod para R esta diseñado para la asistencia quantitativa de los traders en el desarrollo de sus estrategias y modelos financieros.

3.1 ¿Que es quantmod?

Un entorno rápido, donde los operadores cuantitativos pueden explorar y construir modelos de negociación rápida y limpiamente. A través de la función getSymbols podemos extraer datos financieros desde varias fuentes: Google Finance, Yahoo Finance, Federal Reserve Bank of St. Louis FRED (más de 11,000 series !!!) y Oanda. Incluso desde fuentes propias: MySQL , R (Rdata) y Comma Separated Value files (csv).

No es el paquete definitivo dado que se complementa con otros, tales como: TTR, zoo y xts. En lo que respecta al análisis técnico son las más usadas en el mercado y usan todas las propiedades que hacen al lenguaje R útil para realizar análisis de datos¹.

3.2 Obtención de Datos

Para comenzar, como todo paquete en R se debe instalar

# Instalación package
install.packages("quantmod")

Una vez que esté instalado, creamos nuestro script usando ctrl/cmd + shift + n y lo “llamamos” con

# Cargamos "quantmod"
library("quantmod")

HINT: con ctrl + R en windows/Linux y cmd + R en MAC OS agregamos más rapido comentarios (sección) en Rstudio.

quantmod provee una función para descargar datos desde fuentes externas. Esta función se llama getSymbols, para mayor información escribir en la linea de comandos ?getSymbols². Por defecto, se crea un objeto en el workspace (Global Environment) con el nombre del ticker/nemotécnico seleccionado. Imaginemos por un momento que necesitamos analizar el S&P 500 desde el 2010 hasta la fecha con periocidad diaria. Lo primero que debemos hacer es pensar desde que fuente vamos a descargar los datos, como es un índice accionario se recomienda usar yahoo finance, luego buscar el nemotécnico, en este caso es “^GSPC”.

getSymbols("^GSPC", src = "yahoo", from = "2010-01-01", to = "2010-07-30", periodicity = "daily")

## [1] "^GSPC"

3.2.1 ¿Qué hizo la función getSymbols?

La función getSymbols se construye basicamente de cinco opciones³:

1. El ticker/nemotécnico, eg. ^GSPC.
2. src, que es la abreviación de “source”, eg. yahoo, FRED…
3. from, es el inicio de la fecha a descargar, tener presente que se incluye la fecha en nuestros datos.
4. to, es el final del periodo para los datos, este no se incluye.
5. periodicity, es la periodicidad de los datos, eg. daily, monthly o yearly, solo algunos datos se ajustan a las tres periodicidades.

En el ejemplo anterior se descargo desde yahoo los datos del S&P 500 desde Enero del 2010 hasta el viernes 27 de Julio del 2018 con periodicidad diaria, construyendo un objeto en formato xts cuyo nombre es GSPC.

Show 102550100 entries

Search:

GSPC.Open	GSPC.High	GSPC.Low	GSPC.Close	GSPC.Volume	GSPC.Adjusted
1116.560059	1133.869995	1116.560059	1132.98999	3991400000	1132.98999
1132.660034	1136.630005	1129.660034	1136.52002	2491020000	1136.52002
1135.709961	1139.189941	1133.949951	1137.140015	4972660000	1137.140015
1136.27002	1142.459961	1131.319946	1141.689941	5270680000	1141.689941
1140.52002	1145.390015	1136.219971	1144.97998	4389590000	1144.97998
1145.959961	1149.73999	1142.02002	1146.97998	4255780000	1146.97998
1143.810059	1143.810059	1131.77002	1136.219971	4716160000	1136.219971
1137.310059	1148.400024	1133.180054	1145.680054	4170360000	1145.680054
1145.680054	1150.410034	1143.800049	1148.459961	3915200000	1148.459961
1147.719971	1147.77002	1131.390015	1136.030029	4758730000	1136.030029

Showing 1 to 10 of 144 entries

Previous12345…15Next

3.3 Graficando con chartSeries

Aún no introducimos la librería ggplot2, sin embargo, quantmod también nos permite graficar.

3.3.1 chartSeries

Para graficar basta con escribir el nombre del objeto con clase (class) xts, en nuestro caso es GSPC que representa al Standard and Poor 500. Si escribimos TA = NULL, charSeries no mostrará el volume⁴

chartSeries(GSPC, TA=NULL)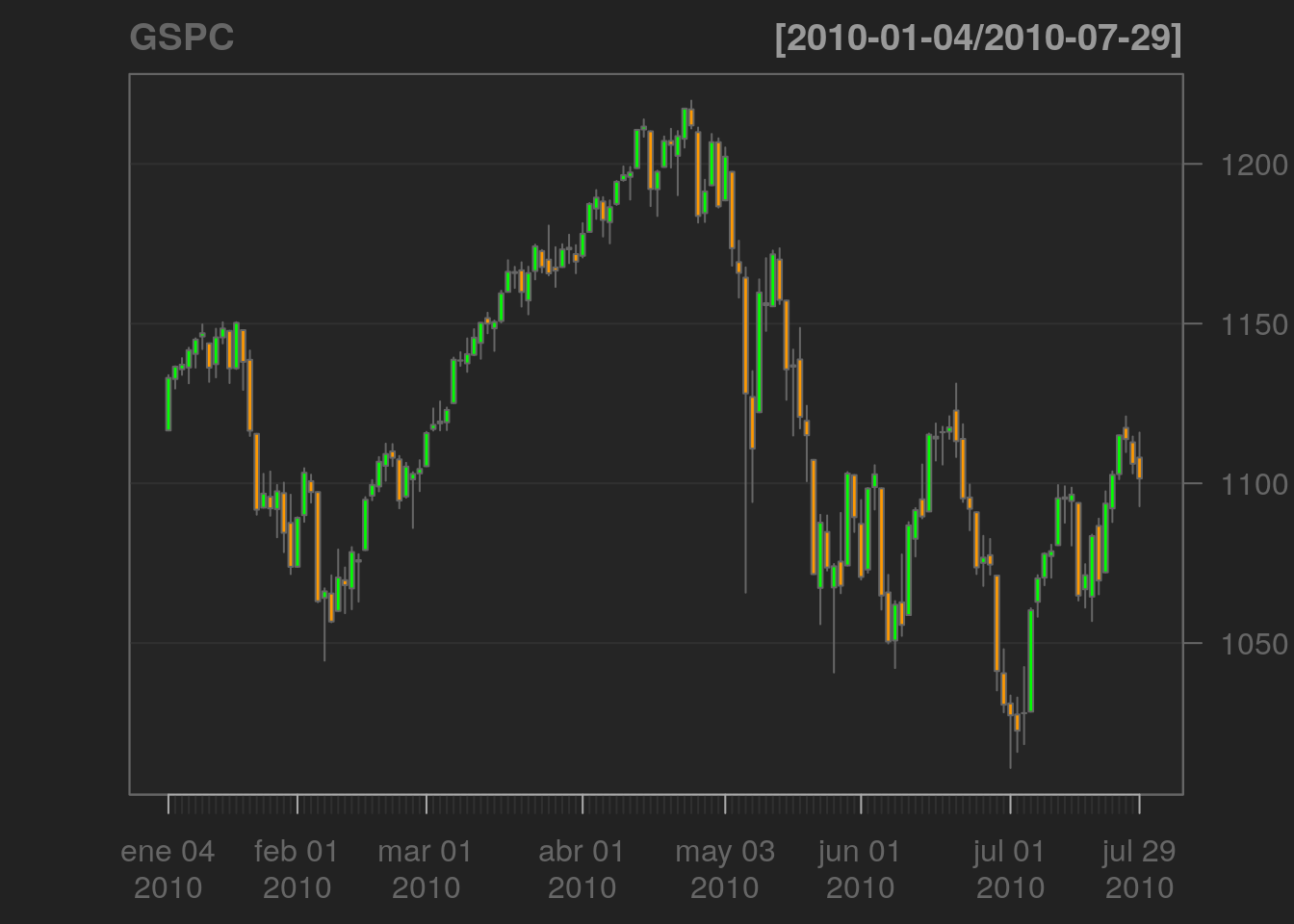

Figure 3.1: Gráfico con chartSeries con TA = NULL

chartSeries(GSPC, TA=NULL)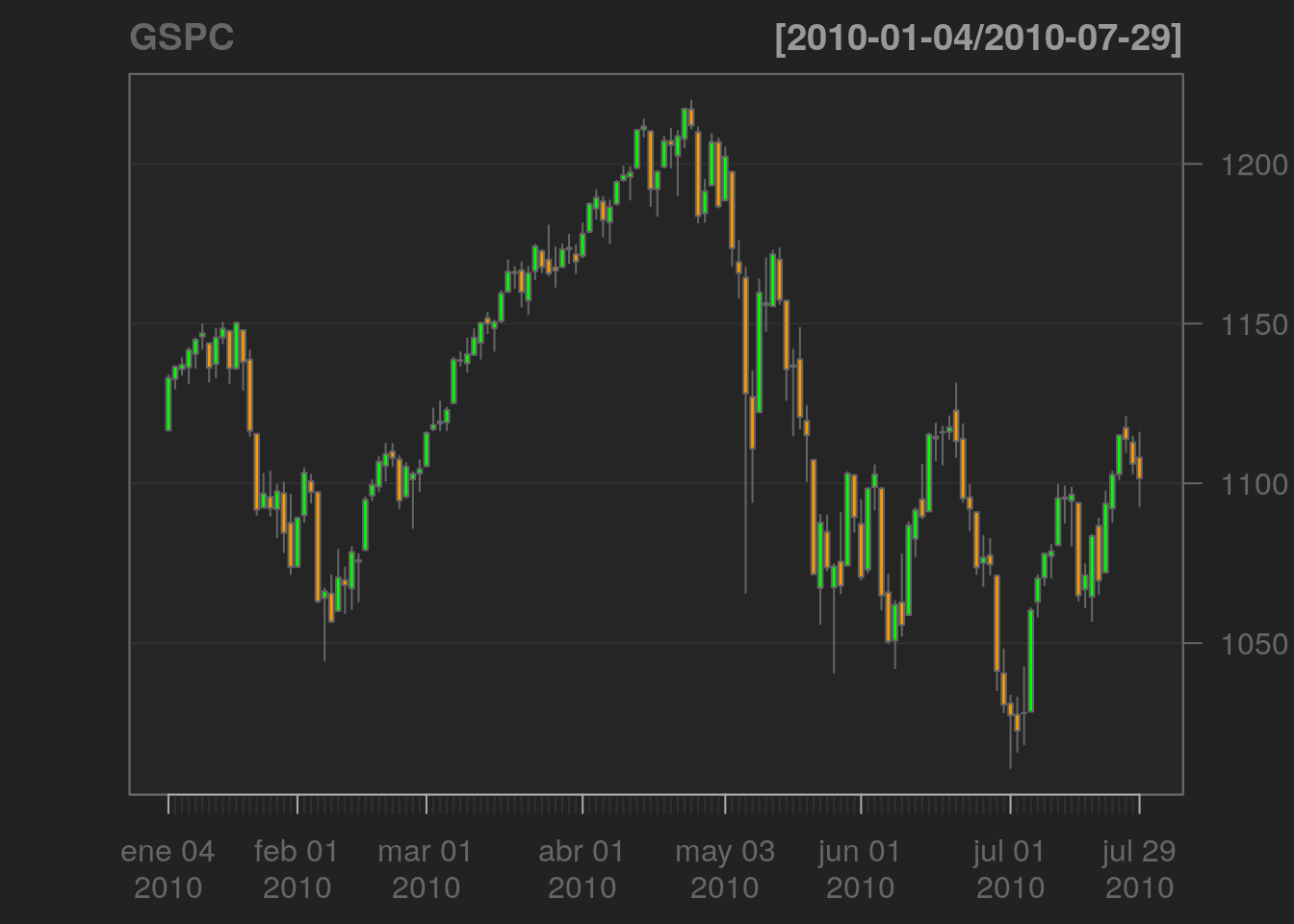

Figure 3.2: Gráfico con chartSeries sin TA = NULL

Pero cuando las series son muy largas, podemos ver tendencias pero dificulta ver cambios importantes a nivel de análisis técnico.

chartSeries(GSPC, subset = "last 3 months")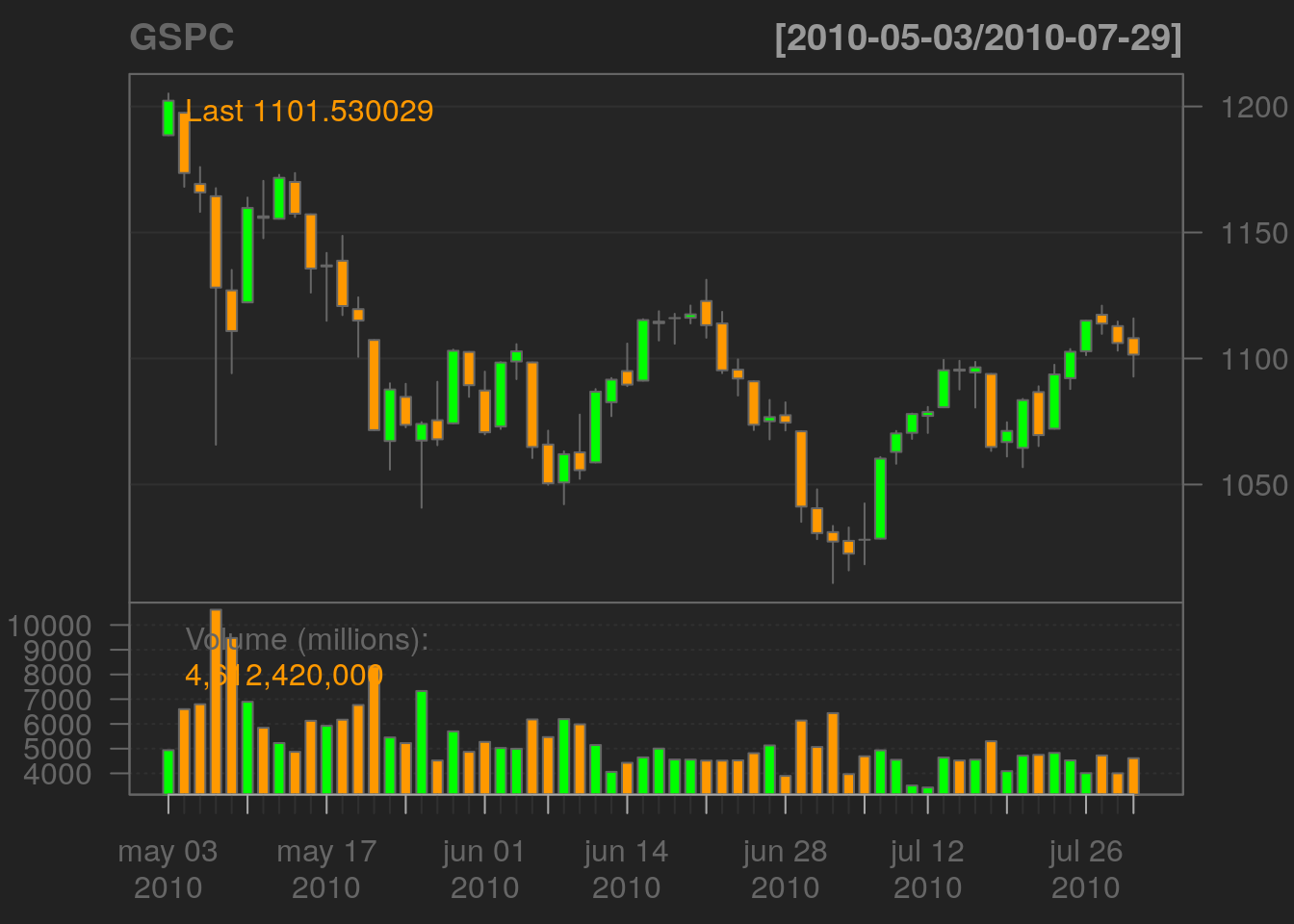

Figure 3.3: Los últimos 3 meses de GSPC

Con el código anterior nos enfocamos solo en los tres meses anteriores.

3.4 Graficando con ggplot2

Si bien chartSeries es una alternativa a plot o plotly, este no nos permite realizar gráficos que se adapten a nuestras necesidades. ¿Qué pasa si queremos graficar retornos o retornos acumulados? la opción por exelencia es ggplot2.

3.4.1 Breve introducción a ggplot2

Todo ggplot2 plot tiene tres componentes:

1. Datos
2. Un conjunto de aesthetic mappings entre variables y propiedades de visualización.
3. Al menos una layer que describe la observación, son usualmente creadas con la función geom_*

library(ggplot2)

A continuación usaremos la base que viene pre cargada con R cuando lo instalamos, que es cars⁵

ggplot(mpg, aes(x = displ, y = hwy)) + geom_point()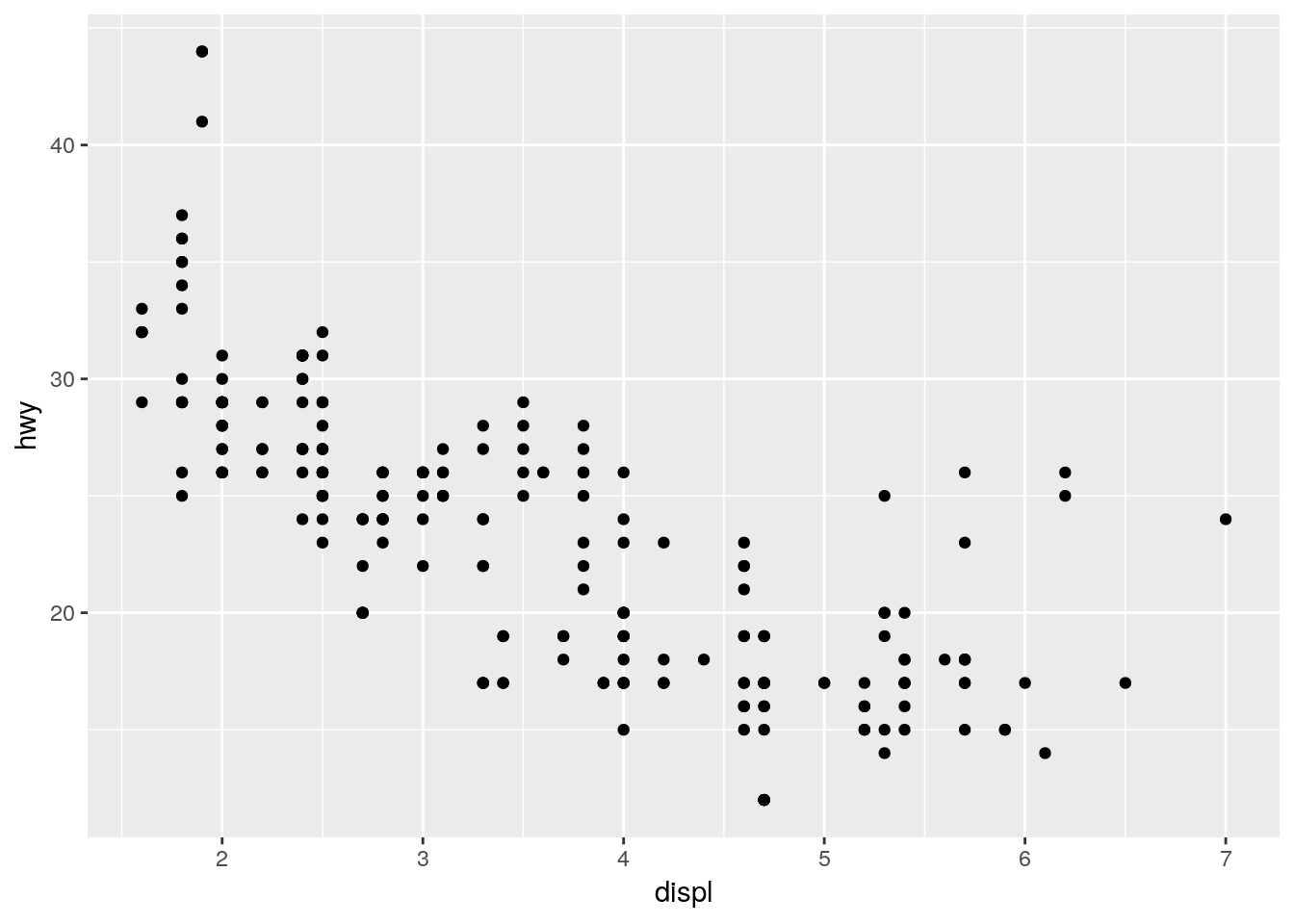

Figure 3.4: Ejemplo 1 usando ggplot2

Esto produce el scatterplot definido como:

1. Datos: mpg
2. Aesthetic mapping: tamaño del motor en la posición x, gasolina en la posición y.
3. Layer: puntos.

3.4.2 Color, tamaño, forma y otros atributos del aesthetic

Se debe usar otro aesthetics como colour, shape y size (ggplot acepta los nombres americanos como británicos)

ggplot(mpg, aes(displ, cty, colour = class)) +
  geom_point()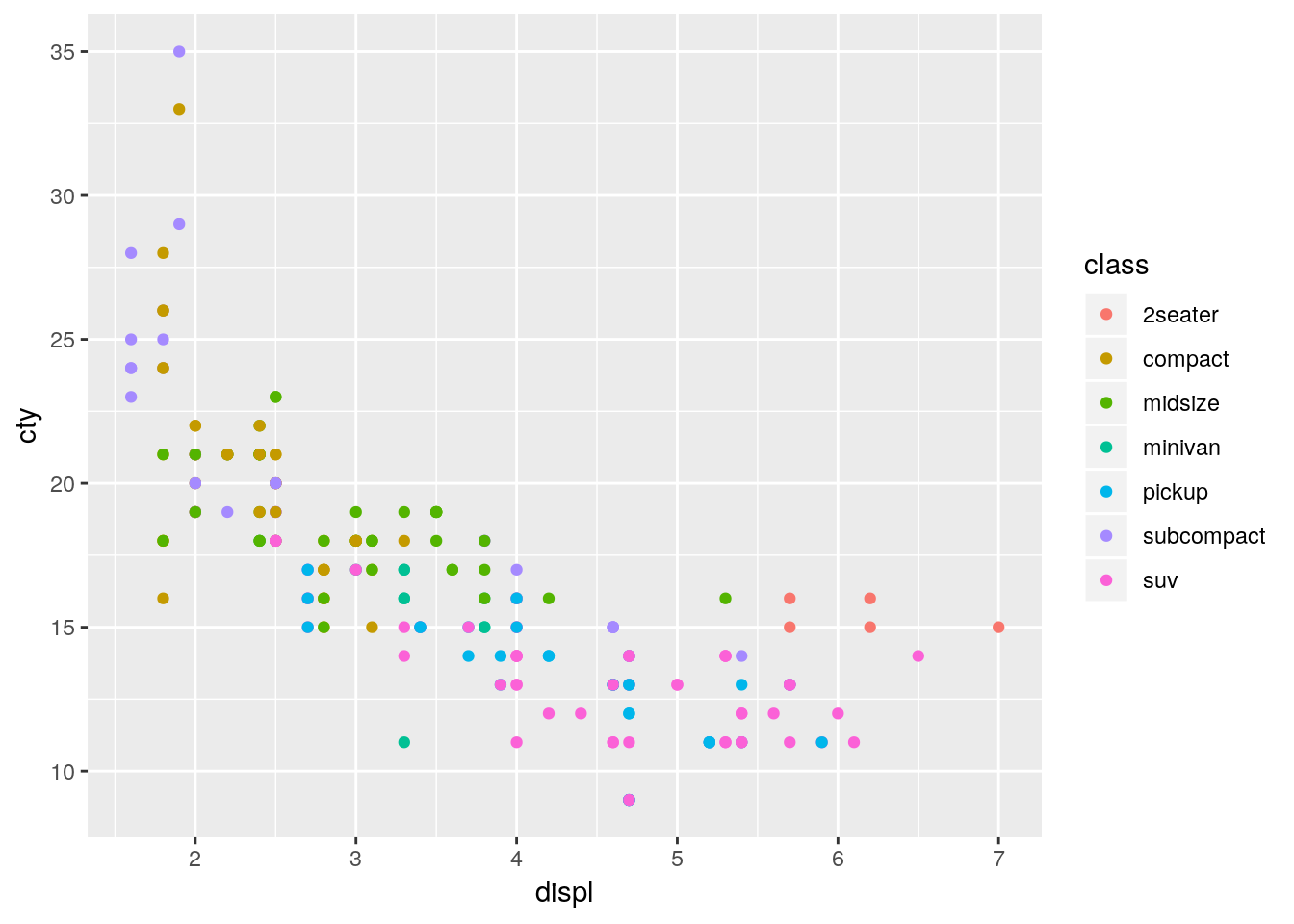 

Figure 3.5: Ejemplo 2 usando ggplot2

• Como se puede ver, se creo una guía con los valores, leyenda, así podemos “leer” el gráfico.
• Si se quiere aesthetic para valores fijos, sin scaling:

ggplot(mpg, aes(displ, hwy)) + geom_point(aes(colour = "blue"))

Figure 3.6: Ejemplo 3 usando ggplot2

ggplot(mpg, aes(displ, hwy)) + geom_point(colour = "blue")

Figure 3.7: Ejemplo 3 usando ggplot2

Ejercicios:

aes(displ, hwy, colour = class)
aes(displ, hwy, shape = drv)
aes(displ, hwy, size = cyl)

• Se recomienda usar colour y shape con variables categóricas.
  
• Mientras que size funciona bien con variables continuas.

3.4.3 S&P 500 con ggplot2

gspc <- as.data.frame(GSPC)

g1 <- ggplot(gspc) + geom_line(mapping = aes(index(gspc),GSPC.Adjusted))
g1 <- g1 + labs(title = "S&P 500", subtitle = "Desde Enero 2010 a 2018") + xlab("Fecha") + ylab("")
g1 <- g1 + theme_bw()
g1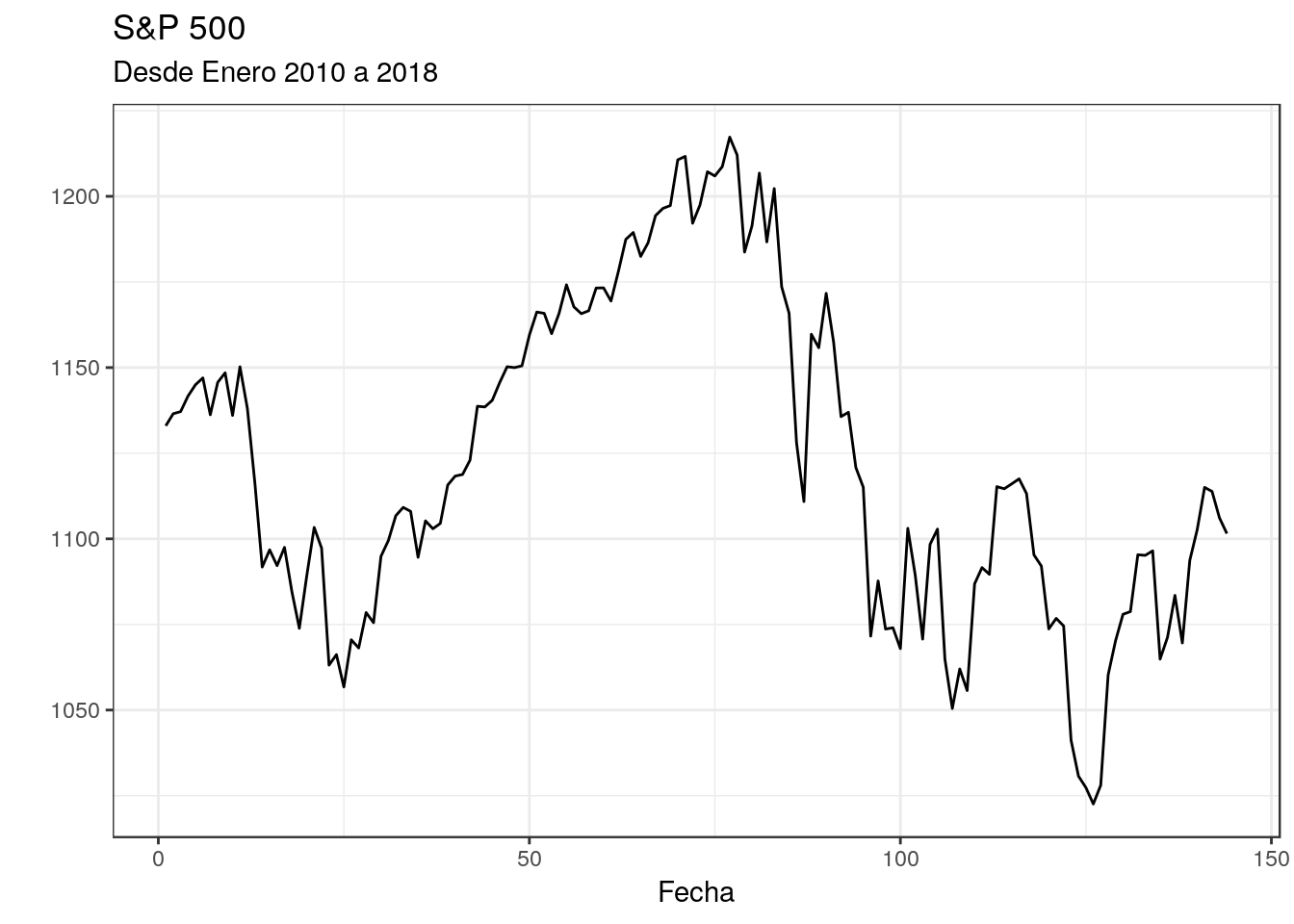

Figure 3.8: Standard and Poor 500 usando ggplot2

3.5 Multiples Datos

A continuación trabajaremos con las acciones de Oracle, Nvidia, IBM y AMD, comenzamos con crear un objeto con los nombres de los tickers

tickers <- c("ORCL","AMD","IBM","NVDA")

descargamos los datos con las características requeridas, que son las mismas que usamos anteriormente con S&P 500

getSymbols(tickers, src = "yahoo", from = "2010-01-01", to = "2018-07-30", periodicity = "daily")

## [1] "ORCL" "AMD"  "IBM"  "NVDA"

Acá deben tener mucha atención:

list <- lapply(tickers, function(x) Cl(get(x)))
precio.cierre <- do.call(merge,list)

3.5.1 Retornos

La formula para calcular (log) retornos es

$$r_t=log(1+R_t)=log\left(\frac{P_t}{P_{t-1}}\right)=p_t-p_{t-1}$$ donde $p_t=log\left(P_t\right)$ es llamado “log price”.

Ahora pasamos a construir el retorno.

retornos <- data.frame(apply(precio.cierre, 2, function(x) Delt(x, type = "log")),
                       fecha = index(precio.cierre)) %>%
            rename(orcl = ORCL.Close, amd = AMD.Close, ibm = IBM.Close, nvda = NVDA.Close) %>% 
            na.omit() 

3.5.2 Retornos Acumulados

Si graficamos los retornos no será muy descriptivo, una forma es trabajar con su acumulado. Con la misma lógica usamos la función cumsum().

acumulados <- data.frame(apply(retornos[1:4], 2, function(x) cumsum(x)), fecha = index(precio.cierre[-1]))

3.5.2.1 Gráfico retornos acumulados

library("reshape2")

reshape <- melt(acumulados, id.vars = "fecha")

g2 <- ggplot(reshape) + geom_line(mapping = aes(fecha,value, color = variable))
g2 <- g2 + labs(title = "Retornos Acumulados", subtitle = "Oracle, AMD, IBM y Nvidia")
g2 <- g2 + theme_bw() + xlab("Fecha") + ylab("Retornos Acumulados")
g2 <- g2 + scale_color_manual("Tickers", values = c("red","blue","green","orange"))
g2 <- g2 + theme(legend.position = "bottom")
g2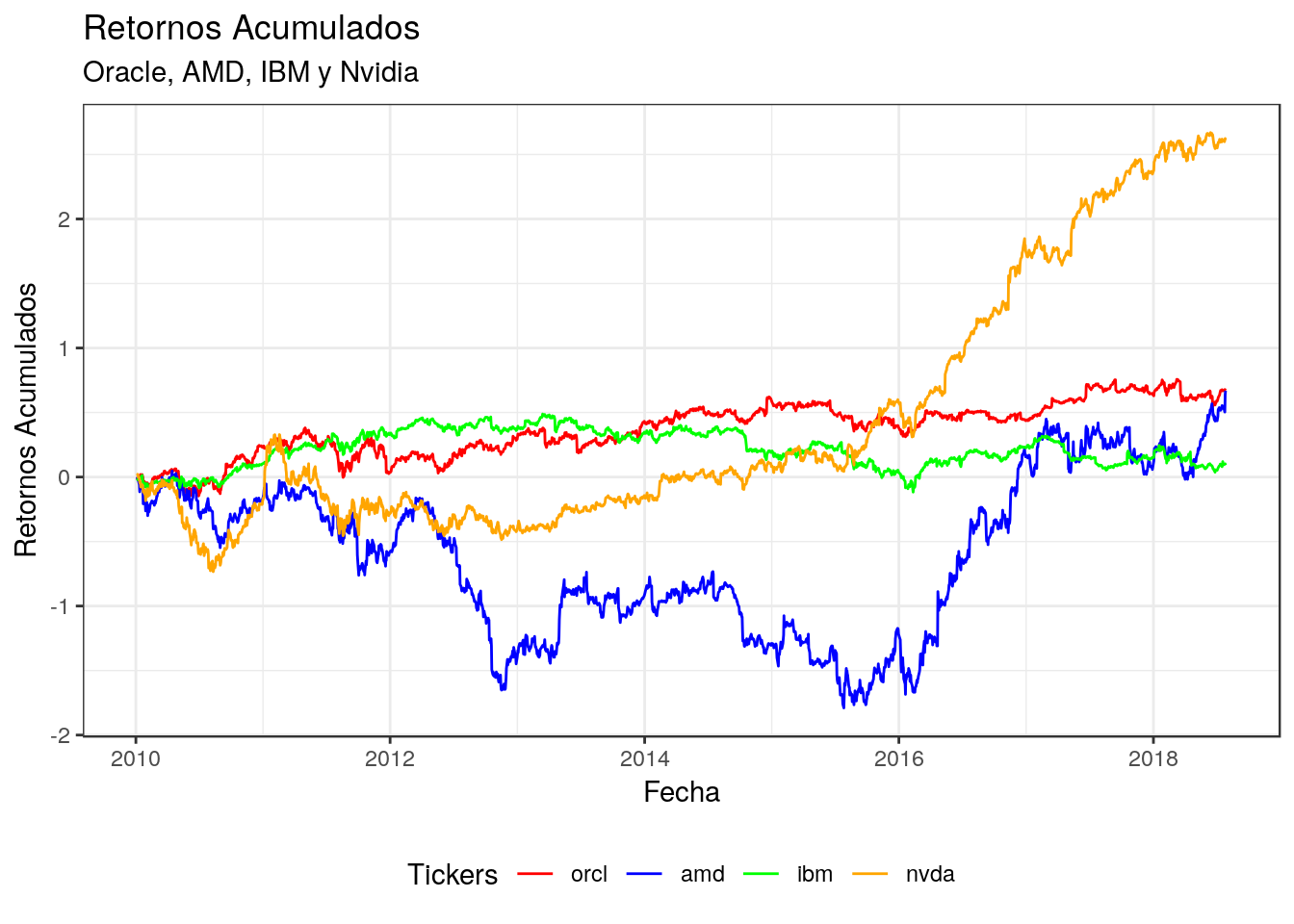

Figure 3.9: Retornos Acumulados de los tickers

3.6 Estadística Descriptiva

Existe muchas formas de obtener la estadística descriptiva en R, un librería es fBasics, la que a su vez contiene test de normalidad.

library("fBasics")

summary <- basicStats(retornos[1:4])[c("Mean", "Stdev", "Median", "Minimum", "Variance",
                                       "Maximum", "nobs","Skewness","Kurtosis"),]

3.7 Ratio de Sharpe

EL ratio de Sharpe es una medida de desempeño para portafolios, el que se define como

$$SR=\frac{E\left(R_i\right)-r_f}{{\sigma }_i}$$

Donde $E\left(R_i\right)={\mu }_i$ es el retorno del portafolio $i$, $r_f$ la tasa libre de riesgo y ${\sigma }_i$ la desviaciòn estandar del portafolio $i$. Si asumimos como ejercicio que no diversificamos y “construimos” cuatro portafolios con el 100% es invertido en cada uno de los activos.

Para realizar el cálculo del ratio de Sharpe (SR) para Oracle

SR_orcl <- (mean(retornos$orcl) - 0.0000 )/sd(retornos$orcl)

con mean(retornos$orcl) vamos a obtener el promedio de la primera columna del objeto retornos que es Oracle (en el data.frame la columna se llama orcl, si tuviese otro nombre como por ejemplo perrito, entonces hubiese sido mean(retornos$perrito)), si quisieramos AMD debería ser amd y asì sucesivamente. El 0.0000 sería la tasa libre de riesgo que la asumimos mensual y sd(retornos[1]) nos calcula la desviación estandar. Dado que poseemos 4 activos con sus respectivos retornos, deberiamos construir cuatro objetos que partan con SR.

3.8 Test de JarqueBera

El test de jarque-bera usa los coeficientes de la skewness y kurtosis de la muestra y se usa para testar normalidad. Otros test comunes son el de Anderson–Darling, Cramér–von Mises, y Kolmogorov–Smirnov.

En resumen compara que la skewness sea 0 y la kurtosis sea 3 bajo normalidad.

$$JB=n{\widehat{Sk}}^2/6+(\widehat{KUr}-3{)}^2/24$$

El test se encuentra en varias librerías, una de ellas es fBasics que deberíamos tener instalada y cargada. Para obtener los resultados del test para Oracle

jarqueberaTest(retornos$orcl)

Para los demàs activos hay que solo cambiar por el nombre de la columna correspondiente.

3.9 Recursos del capítulo

Presentación

3.10 Apéndice

Existe más de una forma de calcular los retornos y retornos acumulados. A continuación cargaremos una base que contiene los precios al cierre desde Enero del 2013 hasta Diciembre del 2018 con periodicidad mensual de las siguientes empresas tecnológicas:

• Facebook (FB)
• Amazon (AMZN)
• Apple (AAPL)
• Netflix (NFLX)
• Google (GOOG)

Ahora en adelante FAANG.

La base de datos se encuentran almacenada en Dropbox en el siguiente enlace

• https://www.dropbox.com/s/tjqvs9w16al1jl2/FAANG.csv?dl=1

Como tiene una extensión csv, utilizamos:

FAANG <- read_csv("https://www.dropbox.com/s/tjqvs9w16al1jl2/FAANG.csv?dl=1")

De esta manera podemos descargarla inmediatamente desde dropbox a nuestra sesión en RStudio.

La base de FAANG contiene las siguientes observaciones.

Show 102550100 entries

Search:

	date	AAPL	AMZN	FB	GOOG	NFLX
1	2013-01-01	65.07	265.5	30.98	375.4	23.61
2	2013-02-01	63.06	264.27	27.25	398.01	26.87
3	2013-03-01	63.24	266.49	25.58	394.53	27.04
4	2013-04-01	63.25	253.81	27.77	409.62	30.87
5	2013-05-01	64.25	269.2	24.35	432.8	32.32
6	2013-06-01	56.65	277.69	24.88	437.34	30.16
7	2013-07-01	64.65	301.22	36.8	441.01	34.93
8	2013-08-01	69.6	280.98	41.29	420.71	40.56
9	2013-09-01	68.11	312.64	50.23	435.12	44.17
10	2013-10-01	74.67	364.03	50.21	511.96	46.07

Showing 1 to 10 of 72 entries

Previous12345…8Next

3.10.1 Retorno y retorno acumulado

La forma en que calcularemos el retorno logarítmico es siguiendo la formula presentado durante el capítulo:

$$r_t=log(1+R_t)=log\left(\frac{P_t}{P_{t-1}}\right)=p_t-p_{t-1}$$

Como tenemos la fecha (date) y el resto de las columnas con los precios, una forma es crear una objeto con tres columnas, fecha (date), symbol (tickers) y precios (prices).

Show 102550100 entries

Search:

	date	symbol	prices
1	2013-01-01	AAPL	65.07
2	2013-02-01	AAPL	63.06
3	2013-03-01	AAPL	63.24
4	2013-04-01	AAPL	63.25
5	2013-05-01	AAPL	64.25
6	2013-06-01	AAPL	56.65
7	2013-07-01	AAPL	64.65
8	2013-08-01	AAPL	69.6
9	2013-09-01	AAPL	68.11
10	2013-10-01	AAPL	74.67

Showing 1 to 10 of 360 entries

Previous12345…36Next

Lo anterior se logra utilizando gather(symbol, prices, -date), luego agrupamos por symbol por medio de group_by(symbol) y creamos el retorno mutate(returns = log(prices/lag(prices))). Como tendremos NA usamos filter(!is.na(returns)), finalmente eliminamos la columna price y extendemos el objeto de tal forma de tener la fecha (date) y las columnas restantes sea el retorno correspondiente a cada tickers (symbol), spread(symbol, returns). Todo lo anterior se resume en el siguiente código:

# retornos 
FAANG_returns <- FAANG %>% 
  gather(symbol, prices, -date) %>% # en la tarea es -Date y no -date
  group_by(symbol) %>% 
  mutate(returns = log(prices/lag(prices))) %>% 
  filter(!is.na(returns)) %>% 
  select(-prices) %>% 
  spread(symbol, returns)

Show 102550100 entries

Search:

	date	AAPL	AMZN	FB	GOOG	NFLX
1	2013-02-01	-0.0314	-0.0046	-0.1283	0.0585	0.1295
2	2013-03-01	0.0029	0.0084	-0.0632	-0.0088	0.0064
3	2013-04-01	0.0003	-0.0488	0.0821	0.0375	0.1324
4	2013-05-01	0.0156	0.0589	-0.1314	0.055	0.046
5	2013-06-01	-0.1259	0.0311	0.0215	0.0104	-0.0694
6	2013-07-01	0.1321	0.0813	0.3914	0.0083	0.1468
7	2013-08-01	0.0739	-0.0696	0.1151	-0.0471	0.1495
8	2013-09-01	-0.0217	0.1068	0.196	0.0337	0.0854
9	2013-10-01	0.092	0.1522	-0.0004	0.1626	0.042
10	2013-11-01	0.0619	0.0781	-0.0659	0.0278	0.126

Showing 1 to 10 of 71 entries

Previous12345…8Next

La lógica para los retornos acumulados es el mismo, pero ahora no debemos trabajar con el objeto FAANG, sino con FAANG_returns.

FAANG_acum <- FAANG_returns %>% 
  gather(symbol, returns, -date) %>% 
  group_by(symbol) %>% 
  mutate(returns_acum = cumsum(returns)) %>% 
  select(-returns) %>% 
  spread(symbol, returns_acum)

3.10.2 Graficar retorno acumulado

FAANG_acum %>% 
  gather(symbol, returns_acum, -date) %>% 
  ggplot(aes(y = returns_acum, x = date, color = symbol)) + 
  geom_line(size = 1.5) + 
  labs(title = "Retornos Acumulados", subtitle = "FAANG", color = "") +
  theme_bw() + 
  theme(legend.position = "bottom", legend.direction = "horizontal")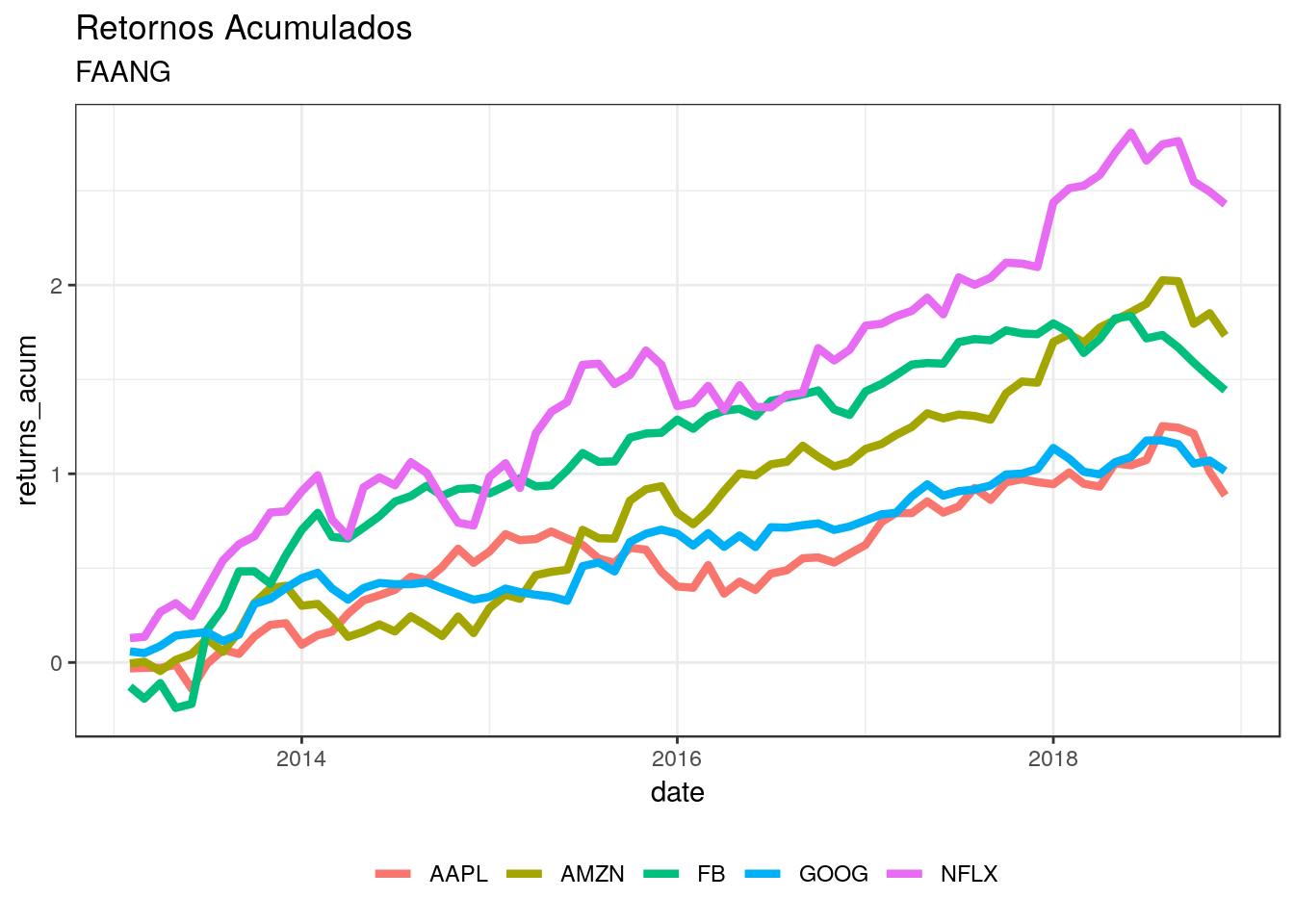 

3.10.3 Teoría de portafolio

Vamos a obtener dos portafolios, el de mínima varianza y el portafolio tangente o media-varianza (optimo).

Comenzamos con cargar las funciones para calcular los portafolios.

library("IntroCompFinR")

Yo “llamé” la librería que instalé con anterioridad, tambíen se puede usar source("IntroCompFinR.R").

Debemos tener el retorno esperado (promedio), el riesgo (desviación estandar) y la matriz de varianza-covarianza.

mean_FAANG <- apply(FAANG_returns[2:6], 2, mean)
sd_FAANG <- apply(FAANG_returns[2:6], 2, sd)
cov_FAANG <- cov(FAANG_returns[2:6])

3.10.3.1 Portafolio de mínima varianza

port_min_var_FAANG <- globalMin.portfolio(mean_FAANG, cov_FAANG, shorts = TRUE) 

El retorno esperado del portafolio de mínima varianza es:

port_min_var_FAANG$er

## [1] 0.01323118

La desviación estandar es:

port_min_var_FAANG$sd

## [1] 0.04743125

y los pesos:

port_min_var_FAANG$weights

##         AAPL         AMZN           FB         GOOG         NFLX 
##  0.294616111 -0.009889592  0.156635553  0.627372021 -0.068734093

3.10.3.2 Portafolio tangente o media-varianza (óptimo)

Necesitamos una tasa libre de riesgo, asumirémos una tasa anualizada del 3%.

risk_free <- 3/1200 # debe estar mensual y no anual

port_tang_FAANG <- tangency.portfolio(mean_FAANG, cov_FAANG, risk_free, shorts = TRUE) 

El retorno esperado del portafolio tangente es:

port_tang_FAANG$er

## [1] 0.02538968

La desviación estandar es:

port_tang_FAANG$sd

## [1] 0.06927247

y los pesos:

port_tang_FAANG$weights

##         AAPL         AMZN           FB         GOOG         NFLX 
##  0.019094873  0.427501514  0.306106748 -0.002029711  0.249326577

3.10.4 Medidas de performance

Veremos dos medidas de performance, Alpha de Jensen y Medida de Treynor, la que aplicaremos solo al último periodo

Ambos se obtienen por medio de la siguiente regresión por mínimo cuadrado ordinario.

$$r_{p,t}-r_{f,t}={\alpha }_p^j+\beta \times (r_{m,t}-r_{f,t})+{\epsilon }_{p,t}$$

Donde $r_{p,t}$ es el retorno del portafolio (en este caso mínima varianza o tangente), $r_{m,t}$ el retorno de mercado (o benchmark), $r_{f,t}$ la tasa libre de riesgo, $\beta$ el componente de riesgo sistemático y ${\alpha }_p^j$ el alfa de jensen.

El $\beta$ no permitirá calcular la medida de Treynor:

$$Treynor=\frac{r_i-r_f}{\beta }$$ Donde $r_i$ el valor esperado del portafolio, $r_f$ tasa libre de riesgo.

Como es solo una ejemplo y tenemos solo una tasa libre de riesgo deberemos calcular el retorno del portafolio $r_{p,t}$ y luego restarle la tasa libre de riesgo $r_{f,t}$.

En el caso del portafolio de mínima varianza debemos realizar una sumaproducto de sus pesos y el retorno en cada periodo.

exceso_min_var <- as.matrix(FAANG_returns[2:6])%*%port_min_var_FAANG$weights - risk_free 

Para el portafolio tangente es el mismo procedimiento.

exceso_tangency <- as.matrix(FAANG_returns[2:6])%*%port_tang_FAANG$weights - risk_free

Solo estaría faltando un benchmark, como es un ejemplo, voy a considerar Google (GOOG), que es la columna 5 de mis retornos.

exceso_benchmark <- as.matrix(FAANG_returns[,5]) - risk_free

Ahora solo nos faltaría hacer la regresiòn para cada portafolio.

Portafolio de minima varianza:

regresion_min_var <- lm(exceso_min_var ~ exceso_benchmark)
regresion_min_var

## 
## Call:
## lm(formula = exceso_min_var ~ exceso_benchmark)
## 
## Coefficients:
##      (Intercept)  exceso_benchmark  
##         0.002254          0.718859

Nuestro alpha de jensen sería 0.0022543 y nuestra medida de Treynor

treynor_min_var <- (mean(exceso_min_var)/coef(regresion_min_var)[2])
treynor_min_var

## exceso_benchmark 
##       0.01492807

Para portafolio tangente:

regresion_tangency <- lm(exceso_tangency ~ exceso_benchmark)
regresion_tangency

## 
## Call:
## lm(formula = exceso_tangency ~ exceso_benchmark)
## 
## Coefficients:
##      (Intercept)  exceso_benchmark  
##          0.01357           0.78993

Nuestro alpha de jensen sería 0.0022543 y nuestra medida de Treynor

treynor_tangency <- (mean(exceso_tangency)/coef(regresion_tangency)[2])
treynor_tangency

## exceso_benchmark 
##       0.02897672

---

1. Proximamente incluire el tidyquant↩

2. No solo funcióna con getSymbols, si no que con todas las funciones de distintas librerias, basta con ante poner ? y luego el nombre la función↩

3. Por el momento solo trabajaremos con estas opciones, exiten más.↩

4. TA proviene de Technical Analysis↩

5. Esta base es muy común en los software estadísticos y presenta datos de autos.↩