Capítulo 4 Renta Fija

IMPORTANTE: Aún no está del todo listo el formato en pdf, por lo que recomiendo verlo online.

if(!require("pacman")) install.packages("pacman")
p_load("tidyverse", "quantmod")

4.1 Precio de un Bono

El precio de un bono se calcula como:

\[ P_{B} = \sum_{t=1}^{T} \frac{C}{(1+r)^t} + \frac{\text{ValorNominal}}{(1+r)^t} \]

Donde:

$P_B$: Precio del Bono
$C_t$: Pago interéses o cupones
$T$ : Números de períodos o madurez
$r$ : Tasa de descuento o yield-to-maturity semi-anual

Consideremos el siguiente ejercicio:

Calcular el precio de un bono con pago de cupón semestral, Madurez 25 años, Tasa cupón 6.5%, Yield semi-anual de 6.9% y Valor nominal de 100.

Para desarrollar el ejercicio, debemos construir por “parte”" los componentes de nuestro bono.

Construimos tanto la tasa cupón como la Yield semi-anual.

tc <- 0.065
y  <- 0.069

Construimos un vector con los valores de los cupones más el principal

pago <- c(rep(tc*100/2,49),(100 + tc*100/2))

tanto tc, r y pago se encontraran en Values del global environment, en tipo numeric. c es una función generica para crear vectores, rep hace una repetición de tc*100/2 49 veces y el numero 50, es igual al principal más tc*100/2. Recordar que como es semi-anual se divide por 2 el valor nominal de 100.

Para poder trabajar con nuestra base de datos, transformamos nuestro vector pago que está en forma numeric a data frame.

pago <- as.data.frame(pago)

Ahora existe un objeto con una estructura de datos data frame en nuestro global environment. Nuestro nuevo objeto pago se podría haber llamado de cualquier forma.

4.2 Dos formas de hacer lo mismo

Ya construido nuestro objeto pago veremos que en R existen muchas formas de hacer lo mismo:

Al principio del capítulo cargamos la libreria tidyverse, está nos permitirá trabajar con un “megapaquete” que incluye otros paquetes en su interior (ggplot2, dplyr, magittr, entre otros). Todos los paquetes que conforman “el Tidyverse” comparten la misma visión sobre el trabajo con datos y la escritura de código. Si vamos a la pestaña packages y escribimos dplyr veremos que está activo, pero nunca lo “llamamos”, esto se debe a tidyverse lo hizo por nosotros.

pago1 <- pago %>% 
         mutate(t1 = as.numeric(index(pago)),factor_desc = 1/(1+y/2)^(t1),
                val_present = pago*factor_desc) %>% 
         summarise(sum(val_present)) %>% 
         rename(`Precio Bono` = `sum(val_present)`)

pago1

##   Precio Bono
## 1       95.27

El precio del bono es 95.2663.

La otra forma es:

# replicamos el objeto
pago2 <- pago

pago2$t2 <- as.numeric(rownames(pago2))

# Calculamos el factor de descuento
pago2$factor_desc <- 1 / (1 + y/2)^(pago2$t2)
# Calculamos el valor presente
pago2$val_present <-  pago2$factor_desc*pago2$pago
# Calculamos el precio
sum(pago2$val_present)

## [1] 95.27

Como es de esperarse obtenemos el mismo precio del bono, 95.2663.

4.3 Funciones

Dominar por completo las funciones en R lleva practica y dedicación, no obstante, la dificultad que utilizaremos en este capítulo es baja y es un buen ejemplo practico para comenzar.

Toda función en R, tiene tres partes.

El body(), el código dentro de la función.
El formals(), la lista de argumentos que controlan como puedes llamar la función.
El environment(), el “mapa” de la locación de las variables de la función.

A continuación vamos a crear un función que permita calcular el cuadrado de cualquier número:

f <- function(x){
    x^2
}

Para obtener el cuadrado de 2 y de 4:

f(2)

## [1] 4

f(4)

## [1] 16

En el ejemplo anterior el formals() de f:

formals(f)

## $x

el body() de f:

body(f)

## {
##     x^2
## }

y el environment() de f:

environment(f)

## <environment: R_GlobalEnv>

Ya visto una breve introducción a funciones en R, procedemos a construir una función que nos permitirá valorizar cualquier bono que pague cupones iguales:

# p: valor nominal; tc: tasa cupón; t: madurez; y: yield to maturity
precio.bono <- function(p,tc,t,y){
  pago   <- c(rep(tc*p, t - 1),p*(1 + tc))
  pago   <- as.data.frame(pago)
  pago$t <- as.numeric(rownames(pago))
  pago$factor_desc <- 1 / (1 + y)^(pago$t)
  pago$valor_prese <- pago$factor_desc*pago$pago
  sum(pago$valor_prese)
}

precio.bono(100,0.065/2,50,0.069/2)

## [1] 95.27

Usando el mismo ejemplo de la sección anterior, obtenermos un precio igual a 95.2663.

4.4 Relación precio del Bono y Yield

4.4.1 Valorización

Ahora utilizando la función precio.bono valorizaremos un bono con las siguientes características:

Principal : 100
Tasa Cupón: 5%
Madurez: 10 años
Yield: 4.29%

# Valoramos el siguiente Bono
precio.bono(p = 100, tc = 0.05, t = 10, y = 0.0429)

## [1] 105.7

4.4.2 Construcción yields

Se contruirá una secuencia de yields:

# Cosntruimos yields 
yields <- seq(0.02, 0.4, 0.01)

La función seq generá una secuencia. En este caso parte del 0.02 hasta el 0.4 pero con intervalos de 0.01.

# Convertimos yields a data frame como antes 
yields <- as.data.frame(yields)

4.4.3 Loops

# Calaculamos el precio del bono para distintas yields
for (i in 1:nrow(yields)) {
  yields$precio[i] <- precio.bono(100, 0.10, 20, yields$yields[i])  
}

4.4.4 Graficando

Una manera de visualizar datos es usar ggplot2, se recomienda que añadan por parte lo que desean en su gráfico.

# Graficamos con ggplot2
g1 <- ggplot(data = yields,aes(x = yields*100, y = precio)) + geom_line(size = 1.5, color = "red") 
g1 <- g1 + geom_point(size = 3, color = "red")
g1 <- g1 + ggtitle("Relación inversa:", subtitle = "Precio del Bono vs Yield")
g1 <- g1 + xlab("Yield (%)") + ylab("Precio del bono") 
g1 <- g1 + geom_ribbon(aes(ymin = 0, ymax = pmax(precio,0)), fill="pink", col="red", alpha=0.5) 
g1 <- g1 + theme_bw() 
g1 <- g1 + theme(panel.border = element_rect(colour = "black", fill = NA, size = .5),
                 panel.grid.major = element_line(colour = "#d3d3d3"))    
g1

Figure 4.1: Relación Bono vs Yield

# Guarmados gráfico
ggsave("retorno-yield.png",width = 8.5, height = 4.5, dpi = 300)

4.5 Trabajando con yields reales

quantmod es uno de las librerías más ocupadas en R para extraer datos financieros, te permite graficar, realizar análisis técnico, calcular retornos (Delt(x)), etc. Aunque las series son descargadas con estructura xts, la podemos transformar a data frame. A continuación descargaremos la yield de los bonos del tesoro de Estados Unidos a 10 años:

t10yr <- getSymbols(Symbols = "DGS10", src = "FRED", auto.assign = FALSE)

t10yr <- subset(t10yr["2000-01-01/2018-04-17"])

Con la función subset extramos una parte de los datos, especificamente desde 2000-01-01 hasta 2018-04-17. Luego graficamos usando la función chartSeries de quantmod. Tener cuidado con la función, dado que solo funciona con extensión xts.

# Grafico con chartSeries de quantmod solo funciona con xts
chartSeries(t10yr,  theme = "white")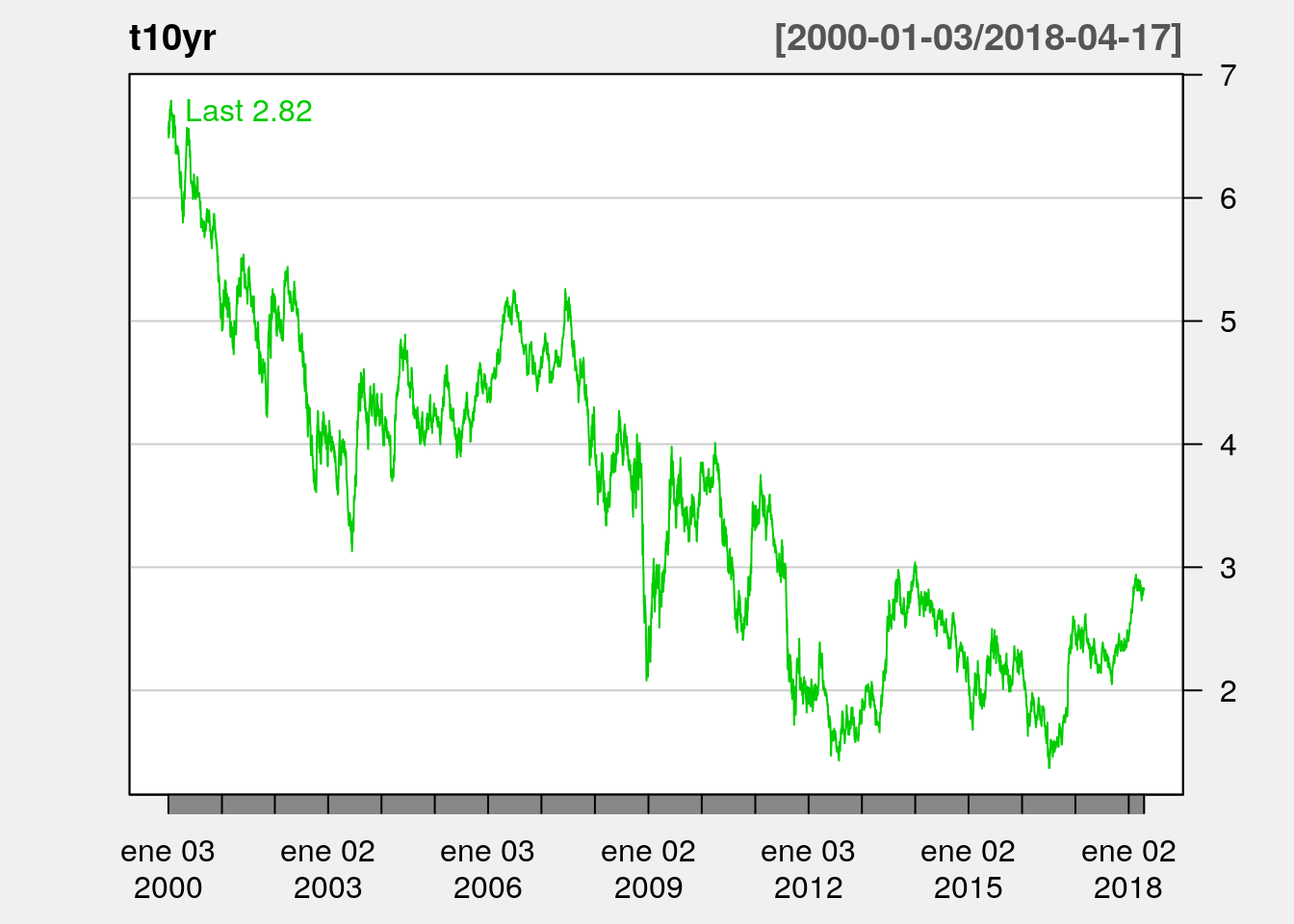

Figure 4.2: yield del tesoro de los Estados Unidos con chartSeries

En caso que se quiera graficar usando ggplot2:

t10yr.df <- as.data.frame(t10yr)

t10yr.df <- t10yr.df %>% 
            mutate(fecha = as.Date(rownames(t10yr.df))) %>% 
            na.omit()

g3 <- ggplot(data = t10yr.df,aes(x = fecha , y = DGS10)) + geom_line(size = 1, color = "green")
g3 <- g3 + ggtitle("10-Year US Treasury Yields", subtitle = "Desde 2000-01-01 hasta 2018-04-17")
g3 <- g3 + ylab("Fecha") +xlab("Yield(%)") 
g3 <- g3 + theme_bw() + theme(panel.border = element_rect(colour = "black", fill = NA, size = .5),
                              panel.grid.major = element_line(colour = "#d3d3d3"))
g3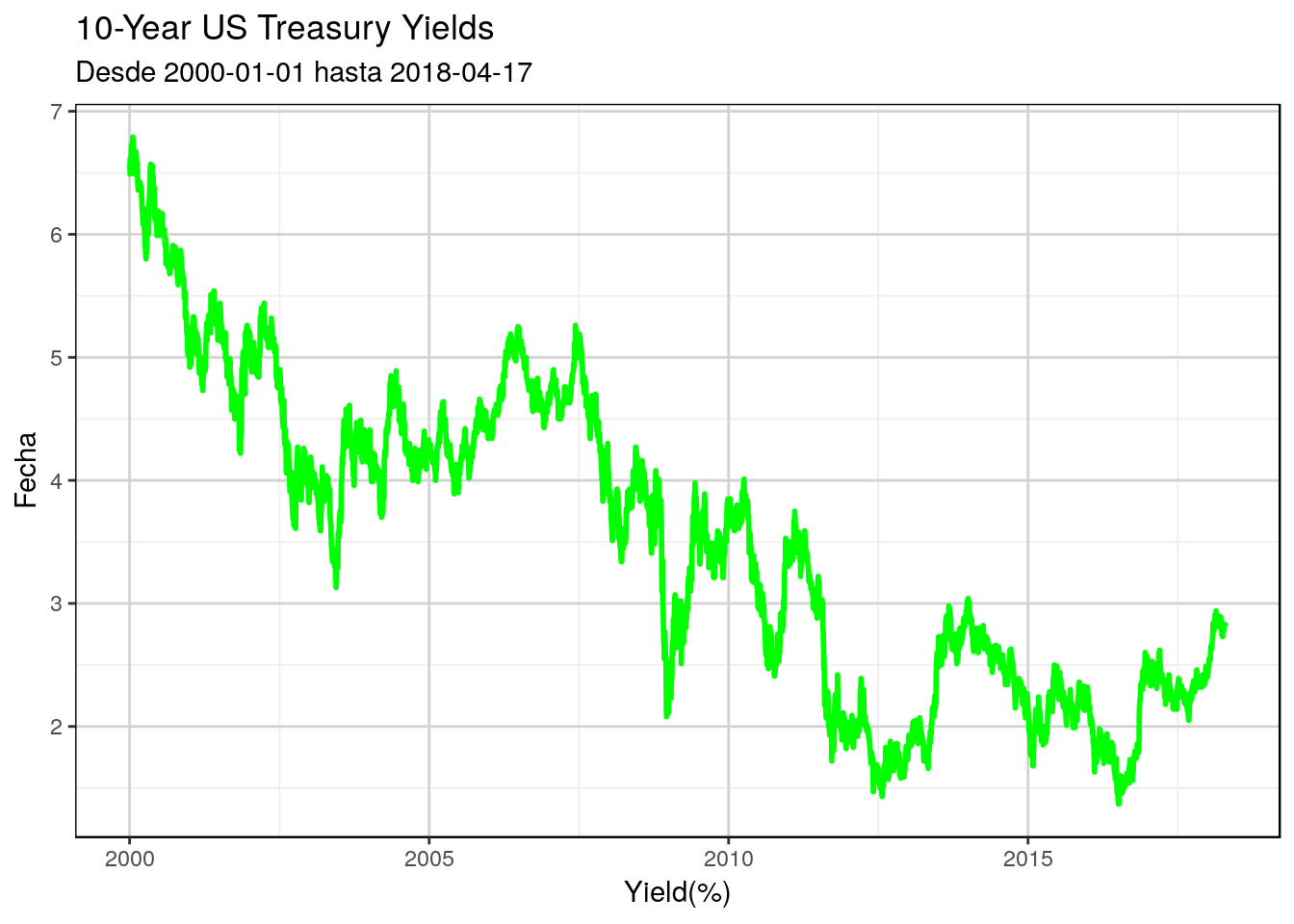

Figure 4.3: yield del tesoro de los Estados Unidos con ggplot2

# Guarmados gráfico
ggsave("treasury-yields.png",width = 8.5, height = 4.5, dpi = 300)

4.6 Duración y Convexidad de un Bono

4.6.1 Extración de la yield

La función subset permite extraer una parte de tu base según un criterio como vimos con anterioridad. En el código presentado a continuación, extraemos un valor de la yield para una fecha en especifico, 2017-03-03 y luego la dividimos por 100.

# Extraemos un valor en específico
t10yr_yield <- t10yr.df %>% 
               subset(fecha == "2017-03-03") 

t10yr_yield <- as.numeric(t10yr_yield$DGS10)*0.01

4.6.2 Duración (Bono Bullet o Americano)

Existen dos Duraciones, la de Macaulay y modificada (o de Hicks), las que miden sensibilidad del precio ante cambios de la yield. Dos bonos con la misma duración tendrá el mismo cambio en precio estimado.

Macaulay:

\[ \text{Duracion de Macaulay} =\bigg[ \frac{1 + y}{y} - \frac{1+y + [n \cdot (c - y)]}{[ c\cdot((1+y)^n - 1)]+y} \bigg] \]

Modificada:

\[ \text{Duracion Modificada} = \text{Duracion de Macaulay}/(1+y) \] Aproximación Duración Modificada:

\[ Aprox.Dur.Mod.= \frac{MV_{-}-MV_{+}}{2 \cdot \Delta y \cdot MV_{0}} \]

4.6.2.1 Duración Macaulay

Como ya presentamos la formula de la duración de Macaulay, la construimos como una función.

# duracion de Macaulay
macaulay <- function(y,n,c,t,T){
         mac <- (1 + y)/y - (1+y+(n*(c-y)))/(c*((1+y)^n -1) + y)
         print(mac)
}

Usandola con la yield extraida:

macaulay <- macaulay(t10yr_yield,10,0.03)

## [1] 8.817

4.6.2.2 Duración Modificada

La aplicación de la duración modificada es directa.

# duración modificada
modificada <- macaulay/(1+t10yr_yield)
modificada

## [1] 8.603

4.6.2.3 Aproximación Duración Modificada

Una aproximación a la duración Modificada se puede obtener como:

# Para la aproximación de la duración modificada
precio.arriba <- precio.bono(p = 100, tc = 0.03, t = 10, y = t10yr_yield + 0.01)
precio        <- precio.bono(p = 100, tc = 0.03, t = 10, y = t10yr_yield)
precio.abajo  <- precio.bono(p = 100, tc = 0.03, t = 10, y = t10yr_yield - 0.01)

Uniendo los objetos creados.

# Calculo de aproximación duración modificada
aprox.dur.mod <- (precio.abajo - precio.arriba)/(2 * precio * 0.01)
aprox.dur.mod

## [1] 8.62

Así obtenemos una diferencia de 0.0169.

4.6.3 Duración con librería

Una librería útil para calcular las duraciones como la convexidad (en la siguiente secciòn) es derivmkts. Si no estamos usando la librería pacman recordar:

install.packages("derivmkts")
library("derivmkts")

# Con librerias
p_load("derivmkts")

# Duración moficada 
duration(precio, 3, 10, 100, 1, modified = TRUE)

## [1] 8.603

# Duración Macaulay
duration(precio, 3, 10, 100, 1, modified = FALSE)

## [1] 8.817

Si escribimos modified = TRUE, la función duration computa la duración modificada, por otro lado, si modified = FALSE obtenemos la duración de Macaulay. Losa valores son los mismo obtenidos sin librería.

4.6.4 Convexidad

La convexidad es la segunda derivada de la curva de rendimiento y es màs precisa que la duración cuando el cambio de la yield es màs “grande”. Esto es porque la duración es la línea tangente en el punto calculado de la curva de rendimientos, el problema es que a medida que nos alejamos por la curva de rendimientos la distancia entre la curva y esa línea calculada se vuelve cada vez más grande.

\[ \text{Convexidad} = \frac{1}{P \times (1+y)^2} \sum_{t=1}^{T} \bigg[ \frac{CF_{t}}{(1 + y)^t } (t^2 + t) \bigg] \]

Donde:

$P$ : Precio Bono.
$y$ : yield to maturity.
$T$ : Madurez en años.
$CF_{t}$ : Cash flow en el tiempo $t$.

# Calculamos medida de convexidad
convexidad <- (precio.arriba + precio.abajo  - 2 * precio)/(precio * (0.01)^2)
convexidad

## [1] 88.45

4.6.4.1 Aproximación Convexidad

La aproximación a la convexidad se puede obtener usando:

\[ \text{Aproximacion Convexidad} = \frac{MV_{-}+MV_{+}-2*MV_{0}}{MV_{0}*\Delta y^2} \]

donde:

$MV_{0}$ : Precio del Bono.
$MV_{-}$ : Precio del Bono cuando la tasa de interes aumenta.
$MV_{+}$ : Precio del Bono cuando la tasa de interes disminuye.
$\Delta y$ : Cambio en la tasa de interes.

4.6.5 Convexidad con librería:

La función convexity de la librería derivmkts permite calcular la convexidad.

convexity(precio, 3, 10, 100, 1)

## [1] 88.34

4.7 Efecto Dolar

El efecto dolar no es más que la suma del cambio (dollar change) del precio del bono ante un cambio marginal de la yield, tanto para la duración como la convexidad.

\[ \text{Efecto Dolar} = \Delta P_{duration} + \Delta P_{convexity} \] Donde:

\[ \text{Duration Dollar Change} = -D \times \Delta y \times P = \Delta P_{duration} \]

Donde:

$D$ : Duración.
$\Delta y$ : Cambio en la yield.
$P$ : Precio Bono.

\[ \text{Convexity Dollar Change} = 0.5 \times C \times (\Delta y)^2 \times P = \Delta P_{convexity} \] Donde:

$C$ : Convexidad.
$(\Delta y)^2$ : Cambio en la yield al cuadrado.
$P$ : Precio Bono.

4.8 Ejercicio

Duración y Convexidad

Un portfolio manager de renta fija nacional ha invertido en un bono a cuatro años de ENERSIS. El instrumento cuenta con una tasa cupón anual de 3 % y un valor nominal de US $100 millones. Adicionalmente sabe que actualmente la tasa de descuento TIR anual es del 8 %. Debido a un aumento en el nivel de precios, el portfolio manager se encuentra preocupado por un eventual incremento en la tasa de interés que fija el Banco Central, por lo tanto recurre a Ud. para que lo asesore ante este posible escenario de alza de tasas.

Calcule la duración y convexidad de este bono.

Calculamos el precio del bono:

precio <- precio.bono(p = 100, tc = 0.03, t = 4, y = 0.08)

La duración es:

duration_mac <- duration(precio, 3, 4, 100, 1, modified = FALSE)
duration_mac

## [1] 3.81

duration_mod <- duration(precio, 3, 4, 100, 1, modified = TRUE)
duration_mod

## [1] 3.528

La convexidad es:

convexity <- convexity(precio, 3, 4, 100, 1)

Utilizando la duración, calcule cuánto bajará de precio el bono ante un aumento de la TIR del 1 % y ante un aumento del 10%. Cómo cambia el resultado anterior si se utiliza convexidad.

Si la variación es de 1 %, la regla de la duración entrega los siguientes resultados:

-duration_mod*0.01

## [1] -0.03528

Si la variación es de 1 %, la regla de la convexidad entrega los siguientes resultados:

-duration_mod*0.01 + 0.5*convexity*(0.01)^2

## [1] -0.03447

Se observa que para variaciones pequeñas ambas medidas entregan resultados muy similares

Por otro lado, si la variación en la TIR es de 10 % la regla de duración arroja los siguientes resultados:

-duration_mod*0.1

## [1] -0.3528

Mientras que para la convexidad se tiene lo siguiente:

-duration_mod*0.1 + 0.5*convexity*(0.1)^2

## [1] -0.2724

Donde se observa que los resultados guardan una diferencia mucho mayor cuando se examina el efecto en el precio de una variación significativa en la tasa de interés

4.9 Apéndice

4.9.1 Bono Frances

El precio del Bono Frances es dístinto al Bono Bullet, dado que amortiza mediante una renta constante de $n$ cuotas.

\[ cuota = C_{0} \times \frac{i \times (1+i)^{n}}{(1+i)^{n}-1} \] donde:

$C_{0}$ = Principañ
$n$ = Duración de la operación en meses, trimestres, semestres o años.
$i$ = Tasa de interés.

En R la función sería:

    precio_frances <- function(p,tc,t,y){
      
      cuota <- p*(tc*(1+tc)^(t))/((1+tc)^(t) - 1)
      
      pago <- c(rep(cuota, t))
      pago <- as.data.frame(pago)
      pago$t <- as.numeric(rownames(pago))
      pago$factor_desc <- 1 / (1 + y)^(pago$t)
      pago$valor_prese <- pago$factor_desc*pago$pago
      sum(pago$valor_prese)
    }

Para calcular la duración y convexidad cambia y no podemos usar la formula mostrada con anterioridad:

Duración Bono Frances:

\[ D = \frac{\sum_{t=1}^{n} C_{t} t (1+r)^{-t}}{\sum_{t=1}^{n} C_{t} (1+r)^{-t}} \]

    duracion_frances <- function(p,tc,t,y){
      
      cuota <- p*(tc*(1+tc)^(t))/((1+tc)^(t) - 1)
      
      pago <- c(rep(cuota, t))
      pago <- as.data.frame(pago)
      pago$t <- as.numeric(rownames(pago))
      pago$arriba <- pago$pago*pago$t*(1+y)^{-pago$t}
      pago$abajo <- pago$pago*(1+y)^{-pago$t}
      duracion <- sum(pago$arriba)/sum(pago$abajo)
      
      print(duracion)
    }

Convexidad Bono Frances:

     convexidad_frances <- function(p,tc,t,y,precio){
    
       # rep returns a vector with value = p * r and times = ttm -1
       cuota <- p*(tc*(1+tc)^(t))/((1+tc)^(t) - 1)
      
       pago <- c(rep(cuota, t))
       pago <- as.data.frame(pago)
       pago$t <- as.numeric(rownames(pago))
       pago$factor_desc <- 1 / (1 + y)^(pago$t)
       pago$valor_prese <- pago$factor_desc*pago$pago*((pago$t)^2 + pago$t)
       print(sum(pago$valor_prese)*(1/(precio*(1+y)^2)))
    }

Introducción a las finanzas quantitativas

Capítulo 4 Renta Fija

4.1 Precio de un Bono

4.2 Dos formas de hacer lo mismo

4.3 Funciones

4.4 Relación precio del Bono y Yield

4.4.1 Valorización

4.4.2 Construcción yields

4.4.3 Loops

4.4.4 Graficando

4.5 Trabajando con yields reales

4.6 Duración y Convexidad de un Bono

4.6.1 Extración de la yield

4.6.2 Duración (Bono Bullet o Americano)

4.6.2.1 Duración Macaulay

4.6.2.2 Duración Modificada

4.6.2.3 Aproximación Duración Modificada

4.6.3 Duración con librería

4.6.4 Convexidad

4.6.4.1 Aproximación Convexidad

4.6.5 Convexidad con librería:

4.7 Efecto Dolar

4.8 Ejercicio

4.9 Apéndice

4.9.1 Bono Frances

4.10 Recursos del capítulo